« Méridien » : différence entre les versions
→Propriétés : Pièce jointe ou pas seul un grand cercle est perpendiculaire à un autre. La méridienne d'un lieu vérifie que les parallèles ne croisent pas à angle droit les méridiens Balises : Modification par mobile Modification par le web mobile |
|||
| (43 versions intermédiaires par 26 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
{{Voir homonymes|Méridien (homonymie)}} |
{{Voir homonymes|Méridien (homonymie)}} |
||
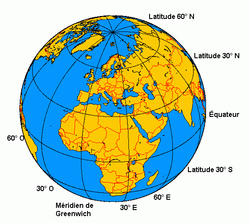
[[Image:Geodesie.png|thumb|Chaque méridien part d'un pôle pour aboutir à l'autre.]] |
[[Image:Geodesie.png|thumb|Chaque méridien géographique part d'un pôle pour aboutir à l'autre.]] |
||
En [[géographie]], un '''méridien''' est une demi-[[ellipse (mathématiques)|ellipse]]{{note| groupe=alpha| Les méridiens ont d'abord été définis comme faisant le tour du [[globe terrestre]]. C'est ainsi qu'à la fin du {{s-|xviii}} on a défini le [[mètre]] comme la {{formatnum:10000000}}{{e}} partie du {{souligner|quart}} de méridien, là où l'on dirait aujourd'hui (mais la définition du mètre a changé) la {{formatnum:10000000}}{{e}} partie d'un {{souligner|demi-}}méridien.}} imaginaire tracée sur le [[globe terrestre]] reliant les [[Pôle géographique|pôles géographiques]]<ref>{{CNRTL|Méridien|3B}}.</ref>. Tous les points de la [[Terre]] situés sur un même méridien ont la même [[longitude]]. On parle également d'[[arc de méridien]] entre deux [[point (géométrie)|points]] ayant une [[latitude]] différente. |
|||
En [[astronomie]], un '''méridien''' est un [[grand cercle]] imaginaire tracé sur la [[sphère céleste]], passant par les [[pôle céleste|pôles célestes]]. L'[[ascension droite]], par exemple, est repérée par les méridiens célestes. Le '''méridien''', ou '''plan méridien''', d'un lieu est un grand cercle de la sphère céleste passant par le pôle céleste, le [[Zénith (astronomie)|zénith]] et le [[Nadir (astronomie)|nadir]] du lieu. À [[midi solaire]], le [[Soleil]] est dans le [[plan (mathématiques)|plan]] méridien. |
|||
== Propriétés == |
== Propriétés == |
||
[[Image:TodayYesterday.jpg|thumb|upright|Le [[180e méridien]] aux [[Fidji]], dont la trajectoire se confond à cet endroit avec la ligne de changement de date.]] |
[[Image:TodayYesterday.jpg|thumb|upright|Le [[180e méridien|180{{e}} méridien]] aux [[Fidji]], dont la trajectoire se confond à cet endroit avec la ligne de changement de date.]] |
||
Les méridiens et les [[Parallèle (géographie)|parallèles]] se coupent toujours à [[angle droit]]{{note|groupe=alpha|En tout point d'une [[surface de révolution]] le parallèle (le cercle intersection de la surface avec le plan perpendiculaire à l’axe de révolution passant par ce point) est perpendiculaire au plan du méridien, et donc à toute courbe de ce plan passant par ce même point (dont le méridien lui-même)<ref>[[Théodore Olivier]], ''Cours de Géométrie descriptive: des courbes et des surfaces courbes'', Dalmont, 1844, [https://books.google.fr/books?id=Ukeiib9ljocC&pg=PA35#v=onepage&q&f=false §251]</ref>.}}{{,}}<ref>{{en}} Bill Casselman, {{citation|Any meridian intersects any parallel at a right angle}} dans [http://www.math.ubc.ca/~cass/courses/m309-01a/ting/page1.html#relationships Relationships between meridians and parallels], Map projection p.1, Department of Mathematics, University of British Columbia.</ref>{{,}}<ref>{{citation|Le plan tangent d'une surface de révolution est déterminé par les deux tangentes menées par le point donné à la section méridienne et au cercle [du parallèle], qui se croisent à angle droit en ce point.}} ''in'' {{Ouvrage |
|||
| ⚫ | |||
|prénom1=Jean Nicolas Pierre |
|||
|nom1=Hachette |
|||
|titre=Traité de géométrie descriptive |
|||
|éditeur=Corby |
|||
|année=1828 |
|||
|pages totales=354 |
|||
|passage=38 |
|||
|lire en ligne=https://books.google.fr/books?id=8cVky7lxmSwC&pg=PA38&dq=%22m%C3%A9ridien%22+%22parall%C3%A8le%22+%22plan+tangent%22+%22ellipso%C3%AFde%22+%22angle+droit%22 |
|||
| ⚫ | |||
|url=http://www.est-team.com/documenti/manuali/the_earth.pdf |
|url=http://www.est-team.com/documenti/manuali/the_earth.pdf |
||
|titre=The Earth according to WGS 84; calculated by Sigurd Humerfelt |
|titre=The Earth according to WGS 84; calculated by Sigurd Humerfelt |
||
| Ligne 17 : | Ligne 26 : | ||
}}</ref>.}}. Les méridiens sont des demi-ellipses et, comme [[géodésique]]s, représentent également les plus courtes distances entre deux de leurs points. |
}}</ref>.}}. Les méridiens sont des demi-ellipses et, comme [[géodésique]]s, représentent également les plus courtes distances entre deux de leurs points. |
||
Par convention, il existe sur Terre {{nombre|360 méridiens}} séparés par un degré d'arc. |
Par convention, il existe sur Terre {{nombre|360 méridiens}} séparés par un [[degré d'arc]]. |
||
Au niveau de l'[[équateur terrestre |
Au niveau de l'[[équateur terrestre]], la distance entre deux méridiens<ref group=alpha>Elle est mesurée le long du parallèle à une latitude donnée.</ref> est égale à 1/360{{e}} partie de la longueur de l'équateur, soit approximativement {{nombre|111.3|kilomètres}}. En s'éloignant de l'équateur, cet écart diminue. Il est égal à la 1/360{{e}} partie de l'équateur multipliée par le [[cosinus]] de la latitude. Ainsi, à {{nombre|45|degrés}} de latitude, la distance entre deux méridiens est égale à {{nombre|111.3|kilomètres}} multipliés par le cosinus de {{nombre|45|degrés}}, soit 0,707, ce qui fait approximativement {{nombre|78.7|kilomètres}}. À {{nombre|60|degrés}} de latitude, l'écart entre deux méridiens passe à {{nombre|55.7|kilomètres}}, le cosinus de cette latitude étant égal à 0,5. Aux pôles géographiques, la distance entre les méridiens est nulle puisqu'ils y convergent (cos 90° = 0). |
||
=== Fuseaux horaires === |
=== Fuseaux horaires === |
||
Un [[fuseau horaire]] est une portion de la surface du globe, limitée par deux méridiens que séparent 15° de longitude. Puisqu'un [[jour solaire]] fait {{nombre|24|heures}}, vingt-quatre fuseaux horaires se répartissent sur 360°. Au niveau de l'[[Équateur terrestre|équateur]] chaque fuseau horaire a une largeur égale au quotient de la division de {{unité|40075|km}} par 24, soit approximativement {{unité|1670|km}}. Cette largeur diminue progressivement jusqu'à devenir nulle aux [[Pôle géographique|pôles]]. |
Un [[fuseau horaire]] est une portion de la surface du globe, limitée par deux méridiens que séparent 15° de longitude. Puisqu'un [[jour solaire]] fait {{nombre|24|heures}}, vingt-quatre fuseaux horaires se répartissent sur 360°. Au niveau de l'[[Équateur terrestre|équateur]] chaque fuseau horaire a une largeur égale au quotient de la division de {{unité|40075|km}} par 24, soit approximativement {{unité|1670|km}}. Cette largeur diminue progressivement jusqu'à devenir nulle aux [[Pôle géographique|pôles]]. |
||
=== Mille |
=== Mille marin === |
||
Le [[mille |
Le [[mille marin]] a été défini comme la longueur moyenne d'une [[minute d'arc]] de méridien ; il vaut {{unité|1852|m}}. |
||
=== Méridien d'origine === |
=== Méridien d'origine === |
||
[[Image:Prime meridian.jpg|thumb|upright|Matérialisation du « |
[[Image:Prime meridian.jpg|thumb|upright|Matérialisation du « méridien d'origine » à l'[[Observatoire royal de Greenwich|observatoire de Greenwich]].]] |
||
Si les [[latitude]]s peuvent être mesurées à partir de l'[[Équateur |
Si les [[latitude]]s peuvent être mesurées à partir de l'[[Équateur terrestre|équateur]], il n'existe pas de référence naturelle équivalente pour fixer l'origine des longitudes. Il est donc nécessaire de définir un méridien d'origine, dont les points ont par définition une longitude égale à zéro. |
||
Actuellement, le [[Méridien de référence de l'IERS|méridien d'origine]] pour la plupart des [[système géodésique|systèmes géodésiques]] se trouve à proximité du [[méridien de Greenwich]] qui passe par l' |
Actuellement, le [[Méridien de référence de l'IERS|méridien d'origine]] pour la plupart des [[système géodésique|systèmes géodésiques]] se trouve à proximité du [[méridien de Greenwich]] qui passe par l'[[Observatoire royal de Greenwich|observatoire de Greenwich]], en [[Angleterre]]. Jusqu'au début du {{S-|XX|e}}, différents pays utilisèrent d'autres méridiens d'origine comme le [[méridien de Paris]] en [[France]] (02° 20' 14,025" E), le méridien de [[Berlin]] en [[Allemagne]] (13° 24' E), le méridien de [[Tolède]] en [[Espagne]] ou le méridien d'[[Uppsala]] en [[Suède]]. |
||
En France, le roi [[ |
En France, le roi [[Louis XIII]] prescrivit par ordonnance en 1634 que le premier méridien serait [[Méridien de Ferro|celui dit de l'Île de Fer]] (aujourd'hui île d'[[El Hierro]] dans l'archipel des [[îles Canaries]]), arbitrairement situé à 20°00'00" à l'ouest du méridien de Paris. Cette localisation permettait d'obtenir une longitude positive pour toutes les terres européennes et a été longtemps suivie par plusieurs autres pays. |
||
Choisir un méridien d'origine de longitude 0° implique l'existence d'un [[180e méridien|antiméridien]], situé à l'opposé sur le globe. La [[ligne de changement de date]] suit cet [[antiméridien]] sur la majeure partie de sa longueur. |
Choisir un méridien d'origine de longitude 0° implique l'existence d'un [[180e méridien|antiméridien]], situé à l'opposé sur le globe. La [[ligne de changement de date]] suit cet [[180e méridien|antiméridien]] sur la majeure partie de sa longueur. |
||
=== Méridien et définition du mètre === |
=== Méridien et définition du mètre === |
||
{{article connexe|Histoire du mètre}} |
{{article connexe|Histoire du mètre}} |
||
La première définition du mètre a été édictée par le décret de l'Assemblée Nationale du 30 mars 1793. Il représentait le dix-millionième de la longueur du quart du méridien terrestre de l'époque, qui était considéré comme faisant le tour de la Terre. Cette longueur est d'abord approximative car la référence doit encore être mesurée. [[Jean-Baptiste Joseph Delambre]] et [[Pierre Méchain]] s'attèlent à la mesure de la distance entre [[Dunkerque]] et [[Barcelone]], et après la publication de leur rapport, le |
La première définition du [[mètre]] a été édictée par le décret de l'Assemblée Nationale du {{date-|30 mars 1793}}. Il représentait le dix-millionième de la longueur du quart du méridien terrestre de l'époque, qui était alors considéré comme faisant le tour de la Terre. Cette longueur est d'abord approximative car la référence doit encore être mesurée. [[Jean-Baptiste Joseph Delambre]] et [[Pierre Méchain]] s'attèlent à la mesure de la distance entre [[Dunkerque]] et [[Barcelone]], et après la publication de leur rapport, le mètre étalon est définitivement fixé par la loi du {{nobr|19 frimaire}} {{nobr|an VIII de la République}} ({{date-|10 décembre 1799}}) : |
||
{{Début citation}}ART . {{Ier}} |
{{Début citation}}ART . {{Ier}} |
||
La fixation provisoire de la longueur du mètre, à trois pieds onze lignes quarante-quatre centièmes, ordonnée par les lois des {{Ier}} août 1793 et 18 germinal an III, demeure révoquée et comme non avenue. Ladite longueur, formant la dix-millionième partie de l'[[arc de méridien|arc du méridien]] terrestre compris entre le pôle nord et l'équateur, est définitivement fixée, dans son rapport avec les anciennes mesures, à trois pieds onze lignes deux cent quatre-vingt-seize millièmes.{{Fin citation}} |
La fixation provisoire de la longueur du mètre, à trois pieds onze lignes quarante-quatre centièmes, ordonnée par les lois des {{Ier}} {{date-|août 1793}} et [[Loi du 18 germinal an III|18 germinal an III]], demeure révoquée et comme non avenue. Ladite longueur, formant la dix-millionième partie de l'[[arc de méridien|arc du méridien]] terrestre compris entre le pôle nord et l'équateur, est définitivement fixée, dans son rapport avec les anciennes mesures, à trois pieds onze lignes deux cent quatre-vingt-seize millièmes.{{Fin citation}} |
||
=== Méridien magnétique=== |
=== Méridien magnétique === |
||
C'est un méridien particulier passant par les [[Pôle magnétique|pôles magnétiques]]. |
C'est un méridien particulier passant par les [[Pôle magnétique|pôles magnétiques]]. |
||
=== Frontières === |
=== Frontières === |
||
Certaines frontières entre pays ou régions ont été déterminées par des méridiens, bien que le cas soit moins fréquent que pour les parallèles. En partant vers l'est depuis le méridien de Greenwich, on peut noter : |
Certaines frontières entre pays ou régions ont été déterminées par des méridiens, bien que le cas soit moins fréquent que pour les parallèles. En partant vers l'est depuis le méridien de Greenwich, on peut noter : |
||
* [[20e méridien est|{{20e}} méridien est]] : partie de la frontière entre la [[Namibie]] et l'[[Afrique du Sud]] et le [[Botswana]] |
* [[20e méridien est|{{20e}} méridien est]] : partie de la frontière entre la [[Namibie]] et l'[[Afrique du Sud]] et le [[Botswana]] ; |
||
* [[129e méridien est|{{129e}} méridien est]] : frontière entre l'Australie de l'Ouest, le territoire du Nord et l'Australie du Sud |
* [[129e méridien est|{{129e}} méridien est]] : frontière entre l'Australie de l'Ouest, le territoire du Nord et l'Australie du Sud ; |
||
* [[138e méridien est|{{138e}} méridien est]] : frontière entre le territoire du Nord et le Queensland (Australie) |
* [[138e méridien est|{{138e}} méridien est]] : frontière entre le territoire du Nord et le Queensland (Australie) ; |
||
* [[141e méridien est|{{141e}} méridien est]] : frontière entre l'Australie du sud, le sud du Queensland, la Nouvelle |
* [[141e méridien est|{{141e}} méridien est]] : frontière entre l'Australie du sud, le sud du Queensland, la Nouvelle-Galles du sud et l’État de Victoria (Australie) ; |
||
* [[141e méridien ouest|{{141e}} méridien ouest]] : frontière entre l'ouest du Canada, le [[Yukon]], avec l'Alaska à partir du |
* [[141e méridien ouest|{{141e}} méridien ouest]] : frontière entre l'ouest du Canada, le [[Yukon]], avec l'Alaska à partir du mont Saint-Elias et au nord de ce sommet jusqu'à l'[[océan Arctique]] ; |
||
* [[120e méridien ouest|{{120e}} méridien ouest]] : frontière entre le Nevada et le nord de la Californie, au sud [[42e parallèle nord|42{{e}}]] parallèle nord |
* [[120e méridien ouest|{{120e}} méridien ouest]] : frontière entre le Nevada et le nord de la Californie, au sud [[42e parallèle nord|42{{e}}]] parallèle nord ; |
||
* [[109e méridien ouest|{{109e}} méridien ouest]] : frontière entre le [[Colorado]] et l'[[Utah]] entre les [[37e parallèle nord|37{{e}}]] et [[41e parallèle nord|41{{e}}]] parallèles nord et entre le [[Nouveau-Mexique]] et l'[[Arizona]] au sud du {{37e}} parallèle nord. L'intersection du {{109e}} méridien ouest et du {{37e}} parallèle nord à [[Four Corners (États-Unis)|Four Corners]] est l'unique point où quatre États se touchent |
* [[109e méridien ouest|{{109e}} méridien ouest]] : frontière entre le [[Colorado]] et l'[[Utah]] entre les [[37e parallèle nord|37{{e}}]] et [[41e parallèle nord|41{{e}}]] parallèles nord et entre le [[Nouveau-Mexique]] et l'[[Arizona]] au sud du {{37e}} parallèle nord. L'intersection du {{109e}} méridien ouest et du {{37e}} parallèle nord à [[Four Corners (États-Unis)|Four Corners]] est l'unique point où quatre États se touchent ; |
||
* [[102e méridien ouest|{{102e}} méridien ouest]] : frontière entre le [[Manitoba]] et la [[Saskatchewan]] et partie de la frontière entre le [[Nunavut]] et les [[Territoires du Nord-Ouest]], au [[Canada]] |
* [[102e méridien ouest|{{102e}} méridien ouest]] : frontière entre le [[Manitoba]] et la [[Saskatchewan]] et partie de la frontière entre le [[Nunavut]] et les [[Territoires du Nord-Ouest]], au [[Canada]] ; |
||
* |
* historiquement la ligne de [[Tordesillas]], située par 46° 37' ouest, a servi à partager les terres encore non explorées par les Européens entre l'[[Espagne]] et le [[Portugal]] lors de la signature du [[traité de Tordesillas]] en 1494. |
||
== Notes et références == |
== Notes et références == |
||
| Ligne 71 : | Ligne 80 : | ||
=== Bibliographie === |
=== Bibliographie === |
||
* Pierre Bayart, ''La Méridienne de France'', l'Harmattan, coll. « acteurs de la science » {{ISBN|978-2-296-03874-5}}, septembre 2007, 252 pages. Préface de [[Jean-Claude Pecker]] (http://www.editions-harmattan.fr/index.asp?navig=catalogue&obj=livre&no=24299 en ligne] |
* Pierre Bayart, ''La Méridienne de France'', l'Harmattan, coll. « acteurs de la science » {{ISBN|978-2-296-03874-5}}, {{date-|septembre 2007}}, 252 pages. Préface de [[Jean-Claude Pecker]] (http://www.editions-harmattan.fr/index.asp?navig=catalogue&obj=livre&no=24299 en ligne] |
||
*Ken Adler, ''Mesurer le monde : L'incroyable histoire de l'invention du mètre'', |
*Ken Adler, ''Mesurer le monde : L'incroyable histoire de l'invention du mètre'', Flammarion , coll. « Libres champs » {{ISBN|978-2081307612}}, {{date-|26 août 2015}}, 660 pages. |
||
=== Articles connexes === |
=== Articles connexes === |
||
| Ligne 88 : | Ligne 97 : | ||
{{DEFAULTSORT:Meridien}} |
{{DEFAULTSORT:Meridien}} |
||
[[Catégorie:Longitude|*Meridien]] |
[[Catégorie:Longitude|*Meridien]] |
||
[[Catégorie:Vocabulaire maritime]] |
[[Catégorie:Vocabulaire maritime]] |
||
Dernière version du 2 avril 2024 à 13:01

En géographie, un méridien est une demi-ellipse[a] imaginaire tracée sur le globe terrestre reliant les pôles géographiques[1]. Tous les points de la Terre situés sur un même méridien ont la même longitude. On parle également d'arc de méridien entre deux points ayant une latitude différente.
En astronomie, un méridien est un grand cercle imaginaire tracé sur la sphère céleste, passant par les pôles célestes. L'ascension droite, par exemple, est repérée par les méridiens célestes. Le méridien, ou plan méridien, d'un lieu est un grand cercle de la sphère céleste passant par le pôle céleste, le zénith et le nadir du lieu. À midi solaire, le Soleil est dans le plan méridien.
Propriétés[modifier | modifier le code]

Les méridiens et les parallèles se coupent toujours à angle droit[b],[3],[4]. Par ailleurs, les méridiens ont tous la même longueur égale à 20 003,931 5 km[c]. Les méridiens sont des demi-ellipses et, comme géodésiques, représentent également les plus courtes distances entre deux de leurs points.
Par convention, il existe sur Terre 360 méridiens séparés par un degré d'arc.
Au niveau de l'équateur terrestre, la distance entre deux méridiens[d] est égale à 1/360e partie de la longueur de l'équateur, soit approximativement 111,3 kilomètres. En s'éloignant de l'équateur, cet écart diminue. Il est égal à la 1/360e partie de l'équateur multipliée par le cosinus de la latitude. Ainsi, à 45 degrés de latitude, la distance entre deux méridiens est égale à 111,3 kilomètres multipliés par le cosinus de 45 degrés, soit 0,707, ce qui fait approximativement 78,7 kilomètres. À 60 degrés de latitude, l'écart entre deux méridiens passe à 55,7 kilomètres, le cosinus de cette latitude étant égal à 0,5. Aux pôles géographiques, la distance entre les méridiens est nulle puisqu'ils y convergent (cos 90° = 0).
Fuseaux horaires[modifier | modifier le code]
Un fuseau horaire est une portion de la surface du globe, limitée par deux méridiens que séparent 15° de longitude. Puisqu'un jour solaire fait 24 heures, vingt-quatre fuseaux horaires se répartissent sur 360°. Au niveau de l'équateur chaque fuseau horaire a une largeur égale au quotient de la division de 40 075 km par 24, soit approximativement 1 670 km. Cette largeur diminue progressivement jusqu'à devenir nulle aux pôles.
Mille marin[modifier | modifier le code]
Le mille marin a été défini comme la longueur moyenne d'une minute d'arc de méridien ; il vaut 1 852 m.
Méridien d'origine[modifier | modifier le code]

Si les latitudes peuvent être mesurées à partir de l'équateur, il n'existe pas de référence naturelle équivalente pour fixer l'origine des longitudes. Il est donc nécessaire de définir un méridien d'origine, dont les points ont par définition une longitude égale à zéro.
Actuellement, le méridien d'origine pour la plupart des systèmes géodésiques se trouve à proximité du méridien de Greenwich qui passe par l'observatoire de Greenwich, en Angleterre. Jusqu'au début du XXe siècle, différents pays utilisèrent d'autres méridiens d'origine comme le méridien de Paris en France (02° 20' 14,025" E), le méridien de Berlin en Allemagne (13° 24' E), le méridien de Tolède en Espagne ou le méridien d'Uppsala en Suède.
En France, le roi Louis XIII prescrivit par ordonnance en 1634 que le premier méridien serait celui dit de l'Île de Fer (aujourd'hui île d'El Hierro dans l'archipel des îles Canaries), arbitrairement situé à 20°00'00" à l'ouest du méridien de Paris. Cette localisation permettait d'obtenir une longitude positive pour toutes les terres européennes et a été longtemps suivie par plusieurs autres pays.
Choisir un méridien d'origine de longitude 0° implique l'existence d'un antiméridien, situé à l'opposé sur le globe. La ligne de changement de date suit cet antiméridien sur la majeure partie de sa longueur.
Méridien et définition du mètre[modifier | modifier le code]
La première définition du mètre a été édictée par le décret de l'Assemblée Nationale du . Il représentait le dix-millionième de la longueur du quart du méridien terrestre de l'époque, qui était alors considéré comme faisant le tour de la Terre. Cette longueur est d'abord approximative car la référence doit encore être mesurée. Jean-Baptiste Joseph Delambre et Pierre Méchain s'attèlent à la mesure de la distance entre Dunkerque et Barcelone, et après la publication de leur rapport, le mètre étalon est définitivement fixé par la loi du 19 frimaire an VIII de la République () :
« ART . Ier La fixation provisoire de la longueur du mètre, à trois pieds onze lignes quarante-quatre centièmes, ordonnée par les lois des Ier et 18 germinal an III, demeure révoquée et comme non avenue. Ladite longueur, formant la dix-millionième partie de l'arc du méridien terrestre compris entre le pôle nord et l'équateur, est définitivement fixée, dans son rapport avec les anciennes mesures, à trois pieds onze lignes deux cent quatre-vingt-seize millièmes. »
Méridien magnétique[modifier | modifier le code]
C'est un méridien particulier passant par les pôles magnétiques.
Frontières[modifier | modifier le code]
Certaines frontières entre pays ou régions ont été déterminées par des méridiens, bien que le cas soit moins fréquent que pour les parallèles. En partant vers l'est depuis le méridien de Greenwich, on peut noter :
- 20e méridien est : partie de la frontière entre la Namibie et l'Afrique du Sud et le Botswana ;
- 129e méridien est : frontière entre l'Australie de l'Ouest, le territoire du Nord et l'Australie du Sud ;
- 138e méridien est : frontière entre le territoire du Nord et le Queensland (Australie) ;
- 141e méridien est : frontière entre l'Australie du sud, le sud du Queensland, la Nouvelle-Galles du sud et l’État de Victoria (Australie) ;
- 141e méridien ouest : frontière entre l'ouest du Canada, le Yukon, avec l'Alaska à partir du mont Saint-Elias et au nord de ce sommet jusqu'à l'océan Arctique ;
- 120e méridien ouest : frontière entre le Nevada et le nord de la Californie, au sud 42e parallèle nord ;
- 109e méridien ouest : frontière entre le Colorado et l'Utah entre les 37e et 41e parallèles nord et entre le Nouveau-Mexique et l'Arizona au sud du 37e parallèle nord. L'intersection du 109e méridien ouest et du 37e parallèle nord à Four Corners est l'unique point où quatre États se touchent ;
- 102e méridien ouest : frontière entre le Manitoba et la Saskatchewan et partie de la frontière entre le Nunavut et les Territoires du Nord-Ouest, au Canada ;
- historiquement la ligne de Tordesillas, située par 46° 37' ouest, a servi à partager les terres encore non explorées par les Européens entre l'Espagne et le Portugal lors de la signature du traité de Tordesillas en 1494.
Notes et références[modifier | modifier le code]
Notes[modifier | modifier le code]
- Les méridiens ont d'abord été définis comme faisant le tour du globe terrestre. C'est ainsi qu'à la fin du xviiie siècle on a défini le mètre comme la 10 000 000e partie du quart de méridien, là où l'on dirait aujourd'hui (mais la définition du mètre a changé) la 10 000 000e partie d'un demi-méridien.
- En tout point d'une surface de révolution le parallèle (le cercle intersection de la surface avec le plan perpendiculaire à l’axe de révolution passant par ce point) est perpendiculaire au plan du méridien, et donc à toute courbe de ce plan passant par ce même point (dont le méridien lui-même)[2].
- Ce calcul correspond à l'ellipsoïde du référentiel géodésique WGS 84[5].
- Elle est mesurée le long du parallèle à une latitude donnée.
Références[modifier | modifier le code]
- Informations lexicographiques et étymologiques de « Méridien » (sens 3B) dans le Trésor de la langue française informatisé, sur le site du Centre national de ressources textuelles et lexicales.
- Théodore Olivier, Cours de Géométrie descriptive: des courbes et des surfaces courbes, Dalmont, 1844, §251
- (en) Bill Casselman, « Any meridian intersects any parallel at a right angle » dans Relationships between meridians and parallels, Map projection p.1, Department of Mathematics, University of British Columbia.
- « Le plan tangent d'une surface de révolution est déterminé par les deux tangentes menées par le point donné à la section méridienne et au cercle [du parallèle], qui se croisent à angle droit en ce point. » in Jean Nicolas Pierre Hachette, Traité de géométrie descriptive, Corby, , 354 p. (lire en ligne), p. 38
- Sigurd Humerfelt, « The Earth according to WGS 84; calculated by Sigurd Humerfelt » [PDF], (consulté le )
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- Pierre Bayart, La Méridienne de France, l'Harmattan, coll. « acteurs de la science » (ISBN 978-2-296-03874-5), , 252 pages. Préface de Jean-Claude Pecker (http://www.editions-harmattan.fr/index.asp?navig=catalogue&obj=livre&no=24299 en ligne]
- Ken Adler, Mesurer le monde : L'incroyable histoire de l'invention du mètre, Flammarion , coll. « Libres champs » (ISBN 978-2081307612), , 660 pages.