Calcul intégral visuel

Le calcul intégral visuel, conçu par Mamikon Mnatsakanian (appelé Mamikon tout court), est une méthode permettant de résoudre rapidement divers problèmes de calcul intégral semblant difficiles à résoudre directement ^[1]. Cette méthode est du type de ce que Martin Gardner appelle un "haha!" ^[2] ou Roger Nelsen une "preuve sans mots" ^[3].

Description[modifier | modifier le code]

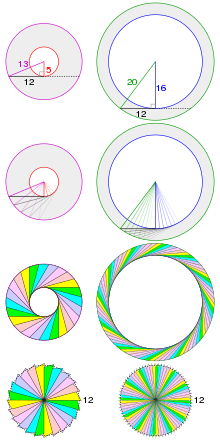
Mamikon a conçu sa méthode en 1959 alors qu'il était encore étudiant, en l'appliquant d'abord à un problème de géométrie bien connu : trouver l'aire d'une couronne, connaissant la longueur d'une corde tangente à la circonférence interne, sans indication supplémentaire.

Le problème se résout facilement à l'aide du théorème de Pythagore mais Mamikon propose une construction originale de la couronne : il dessine d'abord le cercle intérieur, puis déplace un segment tangent de longueur constante le long de sa circonférence, "balayant" ainsi la totalité de la couronne. Il translate ensuite ces segments de manière que leurs points de tangence coïncident ; le résultat est un disque circulaire de rayon connu (et de surface facilement calculable). Mamikon prouve que les deux aires sont égales, ce qui donne la valeur de l'aire de la couronne : $\pi l^{2}/4$ où $l$ est la longueur de la corde.

Plus généralement le théorème de Mamikon concerne l'aire du domaine balayé par un segment $[AB]$ (non forcément de longueur constante) tangent à la courbe décrite par $A$ . Mamikon désigne par "tangent sweep" (traduit pas "balayage tangent") le domaine balayé par le segment et par " tangent cluster" (que nous désignerons par "balayage translaté"), le domaine balayé par un segment $[OM]$ translaté de $[AB]$ , $O$ étant fixe, et énonce alors :

L'aire du balayage tangent est égale à l'aire du balayage translaté, quelle que soit la forme de la courbe d'origine.

Notons que ceci s'applique aussi à une courbe gauche auquel cas le balayage translaté est une portion de cône.

La démonstration précise du théorème se trouve dans ^[1] page 531.

Applications[modifier | modifier le code]

Théorème de Pythagore[modifier | modifier le code]

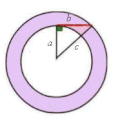
Avec les données de la figure ci-contre, l'aire de la couronne vaut $\pi c^{2}-\pi a^{2}$ ; mais par le théorème de Mamikon, elle vaut $\pi b^{2}$ ; on en déduit bien $c^{2}=a^{2}+b^{2}$ .

Aire d'une arche de cycloïde[modifier | modifier le code]

L'aire d'une arche de cycloïde peut être calculée en considérant la zone qui la sépare d'un rectangle englobant. Les tangentes limitées à ce rectangle peuvent être regroupées pour former un disque (voir la justification plus loin). Si le cercle générant la cycloïde a un rayon $r$ alors ce disque a également un rayon $r$ et une aire $π r 2$ . L'aire du rectangle étant $2 r \times 2π r = 4π r 2$ , l'aire de la cycloïde est $3π r 2$ , soit 3 fois l'aire du cercle générateur.

Le balayage translaté est un disque : en effet considérons le cercle engendrant la cycloïde par roulement ; la tangente à la cycloïde est perpendiculaire au segment joignant le point traçant au point de contact sur la droite de roulement. Ainsi, le segment tangent et le segment précédent forment un triangle rectangle dans le cercle générateur. Cela signifie que, regroupées, les tangentes décrivent bien la totalité du disque intérieur au cercle générateur.

Des solutions à de nombreux autres problèmes se trouvent sur le site "Visual Calculus" ^[5], ainsi que dans ^[6]. Certains sont repris dans l'article ^[7] en français.

Dans ^[8], Tom Apostol décrit comment de jeunes élèves peuvent utiliser cette méthode.

Voir également[modifier | modifier le code]

Le principe de Cavalieri
Le théorème de Holditch, donnant un cas particulier du théorème de Mamikon.

Références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Visual calculus » (voir la liste des auteurs).

↑ ^{a et b} (en) Tom M. Apostol, Mamikon A. Mnatsakanian, « Subtangents -- An Aid to Visual Calculus », The American Mathematical Monthly,‎ jun. - jul., 2002 (lire en ligne)
↑ Martin Gardner, Haha ou l'éclair de la compréhension mathématique, Paris, Pour La Science, 1992
↑ Nelsen, Roger B. (1993). Proofs without Words, Cambridge University Press.
↑ « The Edge of the Universe: Celebrating Ten Years of Math Horizons » (consulté le 9 mai 2017)
↑ Visual Calculus
↑ (en) Tom M. ApostolMamikon A. Mnatsakanian, New Horizons in Geometry, Washington, The Mathematical Association of America, 14 mars 2013, 513 p. (ISBN 978-0-88385-354-2 et 0-88385-354-X, lire en ligne)
↑ J. Bair, V. Henry, « Sur le théorème de Mamikon », Losanges, N°12, SBPMef,‎ 2011 (lire en ligne)
↑ A VISUAL Approach to CALCULUS problems An introduction by Tom Apostol

Lien externe[modifier | modifier le code]

Illustration du calcul de l'aire de la cycloïde

[:1-1] {a et b} (en) Tom M. Apostol, Mamikon A. Mnatsakanian, « Subtangents -- An Aid to Visual Calculus », The American Mathematical Monthly,‎ jun. - jul., 2002 (lire en ligne)

[2] Martin Gardner, Haha ou l'éclair de la compréhension mathématique, Paris, Pour La Science, 1992

[3] Nelsen, Roger B. (1993). Proofs without Words, Cambridge University Press.

[4] « The Edge of the Universe: Celebrating Ten Years of Math Horizons » (consulté le 9 mai 2017)

[:0-5] Visual Calculus

[6] (en) Tom M. ApostolMamikon A. Mnatsakanian, New Horizons in Geometry, Washington, The Mathematical Association of America, 14 mars 2013, 513 p. (ISBN 978-0-88385-354-2 et 0-88385-354-X, lire en ligne)

[7] J. Bair, V. Henry, « Sur le théorème de Mamikon », Losanges, N°12, SBPMef,‎ 2011 (lire en ligne)

[8] A VISUAL Approach to CALCULUS problems An introduction by Tom Apostol

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]