Méthode du carré médian
La mise en forme de cet article est à améliorer ().
La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ».
En mathématiques et en informatique, la méthode du carré médian est une méthode de génération de nombres pseudo-aléatoires. Dans la pratique, il s’agit d’une méthode très imparfaite pour de nombreux objectifs réels, car sa période est généralement très courte et elle présente d'importantes faiblesses ; répétée suffisamment de fois, la méthode du carré du milieu commencera à générer de manière répétée le même nombre ou passera à un nombre précédent dans la séquence et tournera en boucle indéfiniment.
Histoire[modifier | modifier le code]
La méthode a été inventée par John von Neumann qui l'a décrite lors d'une conférence en 1949[1].
Dans son discours de 1949, Von Neumann a plaisanté en disant que « Quiconque considère les méthodes arithmétiques pour produire des chiffres aléatoires est, bien sûr, dans un état de péché ». Ce qu'il voulait dire, a-t-il expliqué, c'est qu'il n'existait pas de véritables « nombres aléatoires », mais simplement des moyens de les produire, et qu'« une procédure arithmétique stricte », comme la méthode du carré médian, « n'est pas une telle méthode ». Néanmoins, il a trouvé ces méthodes des centaines de fois plus rapides que la lecture de nombres « véritablement » aléatoires sur des cartes perforées, ce qui avait une importance pratique pour son travail sur l'ENIAC. Il a trouvé que la « destruction » des séquences de carrés médians était un facteur en leur faveur, car elle est facilement détectable : « on craint toujours l'apparition de cycles courts non détectés »[1]. Nicholas Metropolis a signalé des séquences de 750 000 chiffres avant la « destruction » en utilisant des nombres de 38 bits avec la méthode du « carré médian »[2].
Le livre The Broken Dice d'Ivar Ekeland raconte en détail comment la méthode a été inventée par un frère Franciscain connu uniquement sous le nom de Frère Edvin entre 1240 et 1250[3]. Le manuscrit serait prétendument aujourd'hui perdu, mais Jorge Luis Borges a envoyé à Ekeland une copie qu'il avait réalisée à la Bibliothèque du Vatican.
La modification de l'algorithme du carré du milieu avec une séquence de Weyl[Quoi ?] améliore la période et le caractère aléatoire[4],[5].
La méthode[modifier | modifier le code]
Pour générer une séquence de nombres pseudo-aléatoires à n chiffres, une valeur de départ à n chiffres est créée et mise au carré, ce qui génère un nombre à 2n chiffres. Si le résultat comporte moins de 2 n chiffres, des zéros non significatifs sont ajoutés pour compenser. Les n chiffres du milieu du résultat seraient le numéro suivant dans la séquence et seraient renvoyés comme résultat. Ce processus est ensuite répété pour générer plus de nombres.
La valeur de n doit être paire pour que la méthode fonctionne – si la valeur de n est impaire, il n'y aura pas nécessairement de " n chiffres du milieu" définis de manière unique parmi lesquels sélectionner. Considérez ce qui suit : Si un nombre à 3 chiffres est mis au carré, il peut donner un nombre à 6 chiffres (par exemple 5402 = 291600). S'il devait y avoir un 3 chiffres du milieu, cela laisserait 6 − 3 = 3 chiffres à répartir à gauche et à droite du milieu. Il est impossible de répartir ces chiffres de manière égale des deux côtés du nombre du milieu et il n'y a donc pas de « chiffres du milieu ». Il est acceptable de compléter les graines avec des zéros à gauche afin de créer un nombre pair à n chiffres (par exemple 540 → 0540).
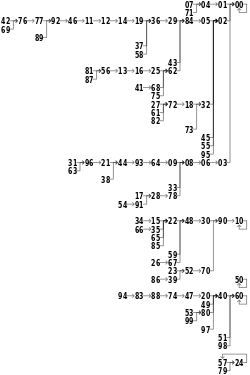
Pour un générateur de nombres à n chiffres, la période ne peut pas dépasser 8n. Si les n chiffres du milieu sont tous des zéros, le générateur génère alors des zéros indéfiniment. Si la première moitié d’un nombre dans la séquence est constituée de zéros, les nombres suivants diminueront jusqu’à zéro. Bien que ces exécutions à zéro soient faciles à détecter, elles se produisent trop fréquemment pour que cette méthode soit utile en pratique. La méthode du carré du milieu peut également rester bloquée sur un nombre autre que zéro. Pour n = 4, cela se produit avec les valeurs 0100, 2500, 3792 et 7600. D'autres valeurs de départ forment des cycles répétitifs très courts, par exemple 0540 → 2916 → 5030 → 3009. Ces phénomènes sont encore plus évidents lorsque n = 2, car aucune des 100 graines possibles ne génère plus de 14 itérations sans revenir à 0, 10, 50, 60 ou à une boucle 24 ↔ 57.
Exemple de mise en œuvre[modifier | modifier le code]
Ici, l'algorithme est rendu en Python 3.11
seed_number = int(input("Veuillez entrer un nombre à 4 chiffres:\n[####] "))
number = seed_number
already_seen = set()
counter = 0
while number not in already_seen:
counter += 1
already_seen.add(number)
number = int(str(number * number).zfill(8)[2:6]) # zfill ajoute un remplissage de zéros
print(f"#{counter}: {number}")
print(f"Nous avons commencé avec {seed_number} et"
f" nous nous sommes répétés après {counter} étapes"
f" avec {number}.")
Références[modifier | modifier le code]
- The 1949 papers were not reprinted until 1951. John von Neumann, “Various techniques used in connection with random digits”, in A. S. Householder, G. E. Forsythe, and H. H. Germond, eds., Monte Carlo Method, National Bureau of Standards Applied Mathematics Series, vol. 12 (Washington, D.C.: U.S. Government Printing Office, 1951): pp. 36–38.
- Donald E. Knuth, The art of computer programming, Vol. 2, Seminumerical algorithms, 2nd edn. (Reading, Mass.: Addison-Wesley, 1981), ch. 3, section 3.1.
- (en) Ivar Ekeland, The Broken Dice, and Other Mathematical Tales of Chance, University of Chicago Press, (ISBN 978-0-226-19992-4)
- Ron Kneusel, Random Numbers and Computers, 1, , 13–14 p.
- (en) Bernard Widynski, « Middle-Square Weyl Sequence RNG », .
